Introduction
Therearealotoftangibleandintangiblequeuingorcrowdingphenomenaindailylife,suchasqueuesforticketpurchasesandbusylocaltelephonelines.Thebasicideaofqueuingtheorywasformedin1909byDanishmathematician,scientist,andengineerA.K.Erlangwhenhesolvedtheproblemofautomatictelephonedesign,whichwascalledthetraffictheoryatthattime.Inspiredbythethermodynamicsstatisticalbalancetheory,hesuccessfullyestablishedatelephonestatisticalbalancemodel,andderivedasetofrecursivestateequations,thusderivingthefamousErlangtelephonelossrateformula.
Sincethebeginningofthe20thcentury,telephonesystemdesignhasbeenapplyingthisformula.Inthe1930s,theSovietmathematicianA.Я.Xinchincalledthetelephonecallflowinstatisticalequilibriumthesimplestflow.SwedishmathematicianBalmintroducedconceptsanddefinitionssuchaslimitedaftereffectflow.Theyusedmathematicalmethodstoanalyzetheintrinsiccharacteristicsoftelephonecallsandpromotedthestudyofqueuingtheory.Intheearly1950s,Americanmathematicianresearchonbirthanddeathprocess,BritishmathematicianD.G.KendallputforwardtheembeddedMarkovchaintheory,andtheclassificationmethodofqueuingqueue,whichlaidthetheoreticalfoundationforqueuingtheory.Afterthis,L.Takakiandothersintroducedthecombinationmethodintoqueuingtheory,makingitmoresuitableforvarioustypesofqueuingproblems.Sincethe1970s,peoplehavebeguntostudyqueuingnetworksandtheasymptoticsolutionsofcomplexqueuingproblems,whichhavebecomeanewtrendinthestudyofmodernqueuingtheory.
Definition
queuingtheory,orstochasticservicesystemtheory,istoobtainthesequantitativeindicators(waitingtime,Queuelength,busyperiod,etc.),andthenimprovethestructureoftheservicesystemorreorganizetheserviceobjectsaccordingtotheselaws,sothattheservicesystemcannotonlymeettheneedsoftheserviceobjects,butalsomaketheorganization’sexpensesthemosteconomicalorSomeindicatorsareoptimal.Itisasub-disciplineofmathematicaloperationsresearchandadisciplinethatstudiestherandomlawofqueuingphenomenaintheservicesystem.Itiswidelyusedinarandomservicesystemforsharingvariousresourcessuchascomputernetworks,production,transportation,andinventory.Thecontentofqueuingtheoryresearchhasthreeaspects:statisticalinference,buildingmodelsbasedondata;systembehavior,thatis,theprobabilisticregularityofquantitativeindicatorsrelatedtoqueuing;systemoptimizationproblems.Itspurposeistocorrectlydesignandeffectivelyoperateeachservicesystemtomakeitplaythebestbenefit.
Thequeuingtheoryoriginatedfromtelephoneconversationsintheearly20thcentury.From1909to1920,theDanishmathematicianandelectricalengineerA.K.Erlangusedthemethodofprobabilitytheorytostudythetelephoneconversationproblem,thuscreatingthisappliedmathematicssubjectandestablishingmanybasicprinciplesforthissubject.Inthemid-1930s,whenW.Fellerintroducedthebirthanddeathprocess,queuingtheorywasrecognizedasanimportantsubjectinmathematics.DuringandafterWorldWarII,queuingtheorybecameanimportantcontentinthenewfieldofoperationsresearch.Intheearly1950s,D.G.Kendallmadeasystematicstudyofqueuingtheory.HeusedtheembeddedMarkovchainmethodtostudyqueuingtheory,whichledtofurtherdevelopmentofqueuingtheory.Itwashewhofirst(1951)usedthethree-lettersymbolX/Y/Ztorepresentaqueuingsystem.WhereXrepresentsthedistributionofcustomerarrivaltime,Yrepresentsthedistributionofservicetime,andZrepresentsthenumberofservicedesksintheserviceorganization.
1. Reprezentace modelu řazení do front
X/Y/Z/A/B/C
X—zákazníci přicházejí jeden po druhémRozděleníčasuintervalu;
Y—distribuce času služby(M—exponenciální rozdělení,D—určitý čas,Ek—k-orderErlangdistribuce,G—obecné rozdělení atd.);
Z—počet servisních stolů;
A—limit kapacity systému(defaultis∞);
B—počet zákaznických zdrojů (výchozí∞);
C – Servisní pravidlo (výchozí je první, kdo je první obsloužený FCFS).
2.Ukazatele měření systému řazení do front
ServicecaptainLs — počet obsluhovaných zákazníků;
QueuelengthLq—počet zákazníků čekajících ve frontě;
Celková délka frontyL=Ls+Lq—celkový početzákazníkůvsystému;
Doba službyWs—Doba spotřebovaná zákazníky v servisu;
Doba čekáníWq—Doba, po kterou zákazník čeká ve frontě;
Celkový časW=Ws+Wq—Zákazník je v systémuCelkový čas pobytu;
Busyperiod—thetimeintervalbetweentwoidletimesoftheserviceorganization;
Intenzita službyρ;
Steadystate—thesystemrunsforalongenoughtimeAfterthat,theinfluenceoftheinitialstatebasicallydisappears,andthesystemstatenolongerchangeswithtime.
3,Výhled na složení a aplikaci systému řazení do front
Thequeuingsystemconsistsofinputprocessandarrivalrules,queuingrules,andserviceTheorganization'sstructure,servicehoursandserviceplanningcomposition.
Generally,itisalsoassumedthattheinter-arrivaltimesequenceandtheservicetimearebothindependentandidenticallydistributedrandomvariablesequences,andthesetwosequencesarealsoindependentofeachother.
Hodnocení kvality systémů řazení do front by mělo být založeno na zájmech jak zákazníka, tak servisní organizace. Pokud jde ozákazníky, vždy se nakupuje tak, abydoba čekánínebodoba pobytubyla co možná nejmenšího počtu. organizacese týká, zvýšení počtu čerpacích stanic znamená zvýšení investic .Pokud se zvýší, bude to způsobovat plýtvání. Pokud se zvýší, způsobí to stížnosti zákazníků nebo dokonce ztracené zákazníky. O kolik je lepší? Aby se zákazníci a servisní organizace starali o své zájmy, musí se postarat o tři ukazatele v systému řazení do front:>>
Theapplicationofqueuingtheoryisveryextensive.Itappliestoallservicesystems.Especiallyincommunicationsystems,transportationsystems,computers,storagesystems,productionmanagementsystems,etc.,itismostwidelyused.Theemergenceanddevelopmentofqueuingtheorycomesfromactualneeds,andactualneedswilldefinitelyaffectitsfuturedevelopmentdirection.
Components
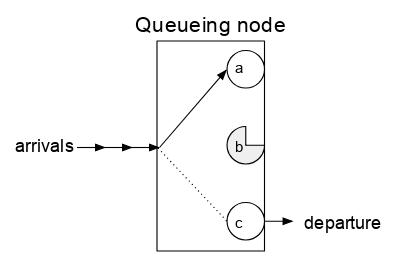
Thequeuingsystemisalsocalledtheservicesystem.Theservicesystemiscomposedofserviceorganizationsandserviceobjects(customers).Thetimewhentheserviceobjectarrivesandthetimetoservehim(thatis,thetimeoccupiedbytheservicesystem)arerandom.Figure1showsthesimplestqueuingsystemmodel.Thequeuingsystemincludesthreecomponents:inputprocess,queuingrulesandserviceorganization.
Theinputprocess
Theinputprocessexaminesthelawofcustomersarrivingattheservicesystem.Itcanbedescribedbythenumberofcustomerarrivalswithinacertainperiodoftimeorthetimeintervalbetweensuccessivearrivalsoftwocustomers.Itisgenerallydividedintotwotypes:deterministicandrandom.Forexample,thepartsprocessedontheproductionlinearriveattheprocessinglocationinturnatthespecifiedintervaltime,andtheregularlyrunningshuttles,flights,etc.arealldeterministicinputs.Stochasticinputmeansthatthenumberofcustomerarrivalsn(t)withintimetobeysacertainrandomdistribution.IfitobeysthePoissondistribution,theprobabilityofreachingncustomerswithintimetis
nebodoba intervaluPro postupně přicházející zákazníky uposlechne záporné exponenciální rozdělení, jmenovitě P(T≤t)=1–e-λt, kdeλje očekávání počtu příchodů zákazníků za jednotku času, což se nazýváprůměrný mezičasλλ; uingtheory ,diskutovaný vstupní proces je převážně náhodný.
Pravidla řazení
Pravidla řazení jsou rozdělena na čekací systém, ztrátový systém a smíšený systém. Když zákazník dorazí, jsou všechny servisní organizace obsazeny a zákazník čeká na lince, což je čekací systém. první, nebo náhodná služba a prioritní služba (např. nemocnice přijímající pohotovostní pacienty). Pokud zákazník přijede a uvidí, že servisní organizace nemůže okamžitě odejít, jedná se oztrátový systém. Některé systémy mají pro zákazníky omezený prostor, aby čekali na linku, takže zákazníci, kteří překročí kapacitumusí opustit systém, je tento systém.
Servisní organizace
Může to být jeden nebo více servisních pultů. Víceservisních pultů může být uspořádáno v paralelních sériích. Servisní doba je obecně rozdělena do dvou typů: deterministický a náhodný. Například zařízení, které automaticky propláchne vůz. henegativní exponenciální rozdělení, funkce rozdělení je P(v≤t)=1–e-μt,kdeμjeprůměrná rychlost službya1/μjePrůměrná doba služby.
Problemsolving
Themainpurposeofstudyingthequeuingsystemproblemistostudyitsoperatingefficiencyandassessthequalityofservice,sothatimprovementmeasurescanbeproposedaccordingly.Thereareusually6quantitativeindicatorsforevaluatingtheprosandconsofaqueuingsystem:
①Systemloadlevelρ:Itisameasureoftheservicedesk'sabilitytoundertakeservicesandmeetneeds;
②Idlepravděpodobnost systémuP0:Systém je s pravděpodobností toho, že nozákazníci vyžádají službu;
③Kapitán:Celkový počet zákazníků čekajících ve frontě na servis a obsluhovaných v systému, je zaznamenána průměrná hodnotaIsLs;
④Kapitán:počet zákazníků čekajících v systému, průměrná hodnota je zaznamenána jako Lg;
⑤Doba pobytu:doba, kterou zákazník zůstává v systému, včetně doby čekání a doby servisu, průměrná hodnota se zaznamená jako Ws;
⑥Waitingtime:acustomerstaysinthesystemTheaveragewaitingtimeinthesystemisrecordedasWg.TheM/M/1queuingsystemisthesimplestqueuingsystem.ThevariousindicatorsofthesystemcanbecalculatedfromthestatetransitionspeeddiagramoftheMarkovchaininthefollowingfigure(Table1).Thecalculationformulasforvariousindicatorsofothertypesofqueuingsystemsaremuchmorecomplicated,andthecalculationformulachartscanbespecificallylistedforreference.Computersimulationhasbeenappliedtosolvetheproblemofqueuingsystem.
Aplikace
Teorie řazení do front je široce používána v dopravních systémech, návrhu přístavišť, údržbě strojů, řízení zásob a dalších servisních systémech. Tabulka2 uvádí aplikace teorie řazení do front.
