jonoteoria

Introduction

Therearealotoftangibleandintangiblequeuingorcrowdingphenomenaindailylife,suchasqueuesforticketpurchasesandbusylocaltelephonelines.Thebasicideaof​​queuingtheorywasformedin1909byDanishmathematician,scientist,andengineerA.K.Erlangwhenhesolvedtheproblemofautomatictelephonedesign,whichwascalledthetraffictheoryatthattime.Inspiredbythethermodynamicsstatisticalbalancetheory,hesuccessfullyestablishedatelephonestatisticalbalancemodel,andderivedasetofrecursivestateequations,thusderivingthefamousErlangtelephonelossrateformula.

Sincethebeginningofthe20thcentury,telephonesystemdesignhasbeenapplyingthisformula.Inthe1930s,theSovietmathematicianA.Я.Xinchincalledthetelephonecallflowinstatisticalequilibriumthesimplestflow.SwedishmathematicianBalmintroducedconceptsanddefinitionssuchaslimitedaftereffectflow.Theyusedmathematicalmethodstoanalyzetheintrinsiccharacteristicsoftelephonecallsandpromotedthestudyofqueuingtheory.Intheearly1950s,Americanmathematicianresearchonbirthanddeathprocess,BritishmathematicianD.G.KendallputforwardtheembeddedMarkovchaintheory,andtheclassificationmethodofqueuingqueue,whichlaidthetheoreticalfoundationforqueuingtheory.Afterthis,L.Takakiandothersintroducedthecombinationmethodintoqueuingtheory,makingitmoresuitableforvarioustypesofqueuingproblems.Sincethe1970s,peoplehavebeguntostudyqueuingnetworksandtheasymptoticsolutionsofcomplexqueuingproblems,whichhavebecomeanewtrendinthestudyofmodernqueuingtheory.

Definition

queuingtheory,orstochasticservicesystemtheory,istoobtainthesequantitativeindicators(waitingtime,Queuelength,busyperiod,etc.),andthenimprovethestructureoftheservicesystemorreorganizetheserviceobjectsaccordingtotheselaws,sothattheservicesystemcannotonlymeettheneedsoftheserviceobjects,butalsomaketheorganization’sexpensesthemosteconomicalorSomeindicatorsareoptimal.Itisasub-disciplineofmathematicaloperationsresearchandadisciplinethatstudiestherandomlawofqueuingphenomenaintheservicesystem.Itiswidelyusedinarandomservicesystemforsharingvariousresourcessuchascomputernetworks,production,transportation,andinventory.Thecontentofqueuingtheoryresearchhasthreeaspects:statisticalinference,buildingmodelsbasedondata;systembehavior,thatis,theprobabilisticregularityofquantitativeindicatorsrelatedtoqueuing;systemoptimizationproblems.Itspurposeistocorrectlydesignandeffectivelyoperateeachservicesystemtomakeitplaythebestbenefit.

Thequeuingtheoryoriginatedfromtelephoneconversationsintheearly20thcentury.From1909to1920,theDanishmathematicianandelectricalengineerA.K.Erlangusedthemethodofprobabilitytheorytostudythetelephoneconversationproblem,thuscreatingthisappliedmathematicssubjectandestablishingmanybasicprinciplesforthissubject.Inthemid-1930s,whenW.Fellerintroducedthebirthanddeathprocess,queuingtheorywasrecognizedasanimportantsubjectinmathematics.DuringandafterWorldWarII,queuingtheorybecameanimportantcontentinthenewfieldofoperationsresearch.Intheearly1950s,D.G.Kendallmadeasystematicstudyofqueuingtheory.HeusedtheembeddedMarkovchainmethodtostudyqueuingtheory,whichledtofurtherdevelopmentofqueuingtheory.Itwashewhofirst(1951)usedthethree-lettersymbolX/Y/Ztorepresentaqueuingsystem.WhereXrepresentsthedistributionofcustomerarrivaltime,Yrepresentsthedistributionofservicetime,andZrepresentsthenumberofservicedesksintheserviceorganization.

1.Jonomallin esitys

X/Y/Z/A/B/C

X—asiakkaatsaapuvat toisen peräänAjanjakauma;

Y – palveluajan jakauma (M – eksponentiaalinen jakautuminen, D – määrätty aika, E_k – k-orderErlang-jakauma, G – yleinen jakelu jne.);

Z—palvelupisteiden lukumäärä;

A—järjestelmän kapasiteettirajoitus(oletus∞);

B—asiakaslähteiden määrä (oletus∞);

C – Palvelusääntö (oletus onensimmäisenä palvellaan ensinFCFS).

2.Jonojärjestelmän mittausindikaattori

PalvelukapteeniL_s –palvelettavien asiakkaiden määrä;

Jonon pituusL_q — jonossa odottavien asiakkaiden määrä;

Jonon kokonaispituusL=L_s+L_q – järjestelmän asiakkaiden kokonaismäärä;

PalveluaikaW_s – Asiakkaan palvelussa käyttämä aika;

OdotusaikaW_q – Aika, jolloin asiakas odottaa jonossa;

KokonaisaikaW=W_s+W_q – Asiakas on järjestelmässäThekokonaisaika;

Busyperiod—thetimeintervalbetweentwoidletimesoftheserviceorganization;

Palveluintensiteettiρ;

Steadystate—thesystemrunsforalongenoughtimeAfterthat,theinfluenceoftheinitialstatebasicallydisappears,andthesystemstatenolongerchangeswithtime.

3,jonojärjestelmän koostumus ja sovellusnäkymä

Thequeuingsystemconsistsofinputprocessandarrivalrules,queuingrules,andserviceTheorganization'sstructure,servicehoursandserviceplanningcomposition.

Generally,itisalsoassumedthattheinter-arrivaltimesequenceandtheservicetimearebothindependentandidenticallydistributedrandomvariablesequences,andthesetwosequencesarealsoindependentofeachother.

Jonojärjestelmien laadun arvioinnin tulisi perustua sekä asiakkaan että palveluorganisaation etuihin. Mitäasiakkaat ovat huolissaan, on aina toivottu, ettäodotusaikataioleskeluaikaonpalvelunmahdollisuuden palveluorganisaatioon huolissaan, palveluasemien määrän lisääminen tarkoittaa investointien kasvua .Joslisää,se aiheuttaa hukkaa.Joslisää,seaiheuttaa asiakkaiden valituksia tai asiakkaita.Kuinka paljon parempi?Jottahuolehditaan omista eduistaan, asiakkaiden ja palveluorganisaatioiden on huolehdittavakolmesta indikaattorista,wai >huollon aika ,näistä kolmesta indikaattorista on tullut jonoteorian tärkein tutkimussisältö.

Theapplicationofqueuingtheoryisveryextensive.Itappliestoallservicesystems.Especiallyincommunicationsystems,transportationsystems,computers,storagesystems,productionmanagementsystems,etc.,itismostwidelyused.Theemergenceanddevelopmentofqueuingtheorycomesfromactualneeds,andactualneedswilldefinitelyaffectitsfuturedevelopmentdirection.

Components

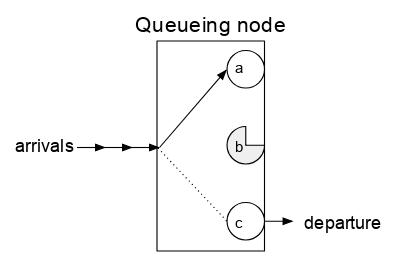
Thequeuingsystemisalsocalledtheservicesystem.Theservicesystemiscomposedofserviceorganizationsandserviceobjects(customers).Thetimewhentheserviceobjectarrivesandthetimetoservehim(thatis,thetimeoccupiedbytheservicesystem)arerandom.Figure1showsthesimplestqueuingsystemmodel.Thequeuingsystemincludesthreecomponents:inputprocess,queuingrulesandserviceorganization.

Theinputprocess

Theinputprocessexaminesthelawofcustomersarrivingattheservicesystem.Itcanbedescribedbythenumberofcustomerarrivalswithinacertainperiodoftimeorthetimeintervalbetweensuccessivearrivalsoftwocustomers.Itisgenerallydividedintotwotypes:deterministicandrandom.Forexample,thepartsprocessedontheproductionlinearriveattheprocessinglocationinturnatthespecifiedintervaltime,andtheregularlyrunningshuttles,flights,etc.arealldeterministicinputs.Stochasticinputmeansthatthenumberofcustomerarrivalsn(t)withintimetobeysacertainrandomdistribution.IfitobeysthePoissondistribution,theprobabilityofreachingncustomerswithintimetis

tai peräkkäinsaapuvien asiakkaiden aikaväli noudattaa negatiivista eksponentiaalista jakaumaa, nimittäin P(T≤t)=1–e^-λt, missäλon asiakkaidensaapumismäärän odotusyksikköaikaa, jota kutsutaanb>väliksikeskiarvoksi.b>keskiarvoksi; Kyselyteoria ,syöttöprosessista keskustellaan pääasiassa satunnaisesti.

Jonosäännöt

Jonosäännöt on jaettu odotusjärjestelmään, menetysjärjestelmään ja sekajärjestelmään. Kun asiakas saapuu, kaikki palveluorganisaatiot ovat varattuja ja asiakas odottaa linjalla, mikä onodotusjärjestelmä. palvellaan,tai viimeksi tullutta palvellaan ensin,tai satunnainen palveluja ensisijainen palvelu (kuten hätäpotilaita vastaanottavat sairaalat).Jos asiakas saapuu ja näkee, että palveluorganisaatio ei ole vapaa lähtemään välittömästi, se onmenetysjärjestelmä. Joissakin järjestelmissä on rajoitetusti tilaa asiakkaiden odotellessa linjaa, asiakkaiden, jotka ylittävät järjestelmän kapasiteetin.

Palveluorganisaatio

Se voi olla yksitai useampia huoltopisteitä.Useita palvelupisteitä voidaan järjestää rinnakkainsarjoissa.Palveluaika on yleensä jaettu kahteen tyyppiin:deterministinen ja satunnainen.Esimerkiksi laite, joka huuhtelee automaattisesti auton. satunnaisjakauma. Jos noudattaa negatiivista eksponentiaalista jakaumaa,jakaumafunktio onP(v≤t)=1–e^{-μt,missäkeskimääräinen palvelunopeusja1/μonKeskimääräinen palveluaika.}

Problemsolving

Themainpurposeofstudyingthequeuingsystemproblemistostudyitsoperatingefficiencyandassessthequalityofservice,sothatimprovementmeasurescanbeproposedaccordingly.Thereareusually6quantitativeindicatorsforevaluatingtheprosandconsofaqueuingsystem:

①Systemloadlevelρ:Itisameasureoftheservicedesk'sabilitytoundertakeservicesandmeetneeds;

②SystemIdleprobabilityP₀:Järjestelmä on todennäköisyydellä, että yksikään asiakas ei pyydä palvelua;

③Kapteeni:Palvelujonossa odottavien ja järjestelmässäpalveltujen asiakkaiden kokonaismäärä,keskimääräinen arvotallennetaanIsL_s;

④Kapteeni:järjestelmässä jonossa odottavien asiakkaiden määrä,keskimääräinen arvo kirjataan L_g;

⑤Viihtymisaika:asiakasoleskeluaikajärjestelmässä, mukaan lukien odotusaika ja palveluaika,keskimääräinen arvo kirjataan W_s;

⑥Waitingtime:acustomerstaysinthesystemTheaveragewaitingtimeinthesystemisrecordedasW_g.TheM/M/1queuingsystemisthesimplestqueuingsystem.ThevariousindicatorsofthesystemcanbecalculatedfromthestatetransitionspeeddiagramoftheMarkovchaininthefollowingfigure(Table1).Thecalculationformulasforvariousindicatorsofothertypesofqueuingsystemsaremuchmorecomplicated,andthecalculationformulachartscanbespecificallylistedforreference.Computersimulationhasbeenappliedtosolvetheproblemofqueuingsystem.

Sovellus

Jonoteoriaa on käytetty laajalti kuljetusjärjestelmissä, satamalaiturin suunnittelussa, koneen huollossa, varastonvalvonnassa ja muissa palvelujärjestelmissä. Taulukossa 2 on lueteltu jonoteorian sovellukset.